誤差逆伝播法

これまでは、ニューラルネットワークの各パラメータについての目的関数の数値微分を計算することで勾配の計算を求める方法を説明しました。
勾配ベクトルの各成分は、各層の結合重みと各ユニットのバイアスでの損失関数の微分です。
しかし、ニューラルネットワークの層数が多くなると、数値微分の計算は膨大な時間がかかるでしょう。さらに、特に入力に近い深い層のパラメータほど、計算の手間が多くなります。
ここで、パラメータの勾配の計算を効率よく行う手法である「誤差逆伝播法」について学びます。
複数の関数によって構成される関数を合成関数と呼びます。
zt=t2=x+y 合成関数の微分は、「tに関するzの微分∂t∂z」と「xに関するtの微分∂1∂t」の積のように、それぞれの関数の微分の積で求められます。
∂x∂z=∂t∂z∂x∂t
dxdy=dudy⋅dxdu に対して、「du が消えるから当然だ」のように考えがちが、その思うのは誤りです。
なぜなら、dxdy、dudy、dxdu はそれぞれ極限を含む定義式であり、単なる分数ではないからです
dudy∣∣u=u0=f′(u0)=Δu→0limΔuf(u0+Δu)−f(u0) dxdu∣∣x=x0=g′(x0)=Δx→0limΔxg(x0+Δx)−g(x0) 微分の定義は:
f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0) これを使うと、
y=f(u), u=g(x) の場合、
dxdy=Δx→0limΔxf(g(x+Δx))−f(g(x)) この極限の中で、
Δu=g(x+Δx)−g(x) を代入して丁寧に展開すると、最終的に
dxdy=f′(u)⋅g′(x) が導かれます。
つまり、この関係は「分数を掛けた」わけではなく、極限に関する計算によって得られるものです。
2線形変換の逆伝播の導出¶
入力データxは(N×D)の行列、Wは(D×H)の行列、bは要素数Hのベクトルと考え、線形変換の計算は以下の式で表します。
y=xW+b=⎝⎛x0,0x1,0⋮xN−1,0x0,1x1,1⋮xN−1,1⋯⋯⋱⋯x0,D−1x1,D−1⋮xN−1,D−1⎠⎞⎝⎛w0,0w1,0⋮wD−1,0w0,1w1,1⋮wD−1,1⋯⋯⋱⋯w0,H−1w1,H−1⋮wD−1,H−1⎠⎞+(b0b1⋯bH−1)=⎝⎛∑d=0D−1x0,dwd,0+b0∑d=0D−1x1,dwd,0+b0⋮∑d=0D−1xN−1,dwd,0+b0∑d=0D−1x0,dwd,1+b1∑d=0D−1x1,dwd,1+b1⋮∑d=0D−1xN−1,dwd,1+b1⋯⋯⋱⋯∑d=0D−1x0,dwd,H−1+bH−1∑d=0D−1x1,dwd,H−1+bH−1⋮∑d=0D−1xN−1,dwd,H−1+bH−1⎠⎞=⎝⎛y0,0y1,0⋮yN−1,0y0,1y1,1⋮yN−1,1⋯⋯⋱⋯y0,H−1y1,H−1⋮yN−1,H−1⎠⎞ ここで、「n番目の出力データのh番目の項yn,h」は、
yn,h=d=0∑D−1xn,dwd,h+bh で計算できるのが分かります。
例えば、損失関数に二乗誤差
L=21∣∣y(x)−d∣∣2 を選んだとき、連鎖律より、∂wd,h∂Lは次の式で求められます
∂wd,h∂L=n=0∑N−1∂yn,h∂L∂wd,h∂yn,h ∂yn,h∂Lは、yn,hに関するLの微分です。
∂wd,h∂yn,hは、wd,hに関するyn,hの微分です。
ここで、∂wd,h∂yn,hは、
∂wd,h∂yn,h=∂wd,h∂{d=0∑D−1xn,dwd,h+bh}=∂xn,d∂{xn,0w0,h+⋯+xn,dwd,h+⋯+xn,D−1wD−1,h+bh}=0+⋯+xn,d+⋯+0+0=xn,d になりますため、
∂wd,h∂L=n=0∑N−1∂yn,h∂Lxn,d 2.2バイアスの勾配¶
同じく連鎖律より、∂bh∂Lは次の式で求められます。
∂bh∂L=n=0∑N−1∂yn,h∂L∂bh∂yn,h ∂bh∂yn,h=∂wd,h∂{d=0∑D−1xn,dwd,h+bh}=0+1=1 まとめると、
∂bh∂L=n=0∑N−1∂yn,h∂L 3ニューラルネットワークにおける誤差逆伝播法の計算例¶
連鎖律より勾配を計算する考え方をニューラルネットワークにも適用する計算例を見ましょう。
具体的には、ニューラルネットワークを構成する関数が持つパラメータについての目的関数の勾配を、順伝播で通った経路を逆向きにたどるようにして途中の関数の勾配の掛け算によって求めます。
ニューラルネットワークには、活性化関数によて変換し、次の層へ伝播するといった計算の流れになりますが、逆伝播による勾配を計算できる原理は変わらないです。
ここから、手計算を通じて誤差逆伝播法の実装を理解しましよう。
i1=0.05,i2=0.10 w1=0.15,w2=0.20,w3=0.25,w4=0.30 w5=0.40,w6=0.45,w7=0.50,w8=0.55 h(x)=1+exp(−x)1 教師データ
o1=0.01,o2=0.99 目的関数は平均二乗誤差関数を用いることにします。
L=N1n=1∑N(tn−yn)2 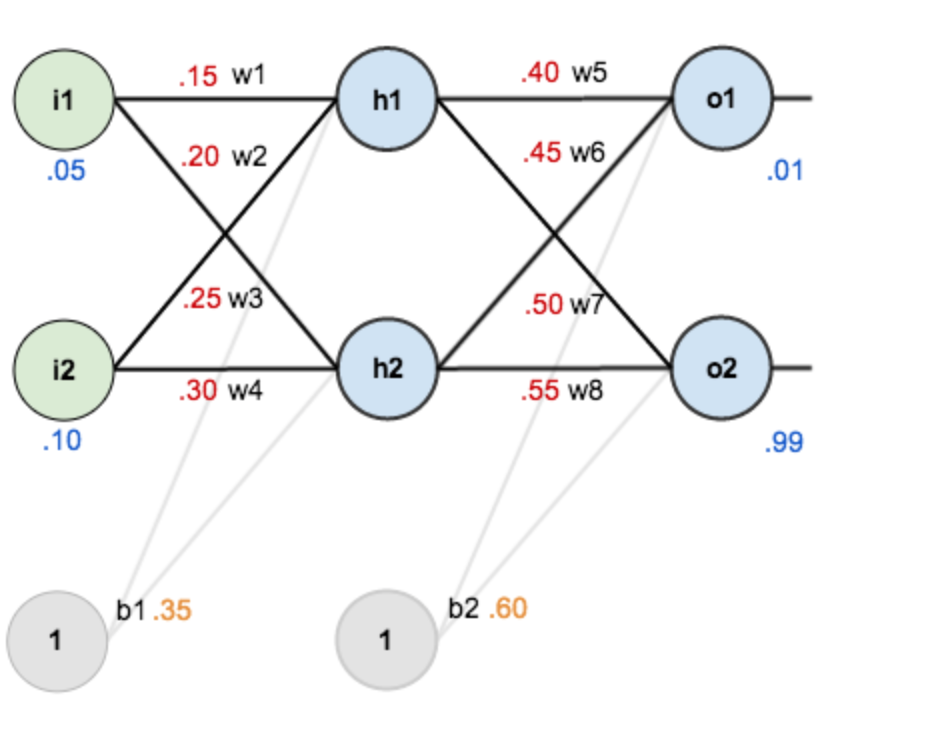
ニューラルネットワークの実装例
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
net_h1= (0.15)*(0.05)+(0.2)*(0.1)+0.35
print("net_h1={}".format(net_h1))
net_h2= (0.25)*(0.05)+(0.3)*(0.1)+0.35
print("out_h2={}".format(net_h2))
out_h2=0.39249999999999996
net_o1 = (0.4)*net_h1+(0.45)*net_h2+0.6
out_o1= sigmoid(net_o1)
print("out_o1={}".format(out_o1))
net_o2 = (0.5)*net_h1+(0.55)*net_h2+0.6
out_o2= sigmoid(net_o2)
print("out_o2={}".format(out_o2))
out_o1=0.7165932011681534
out_o2=0.7319669364891265
L_1 = 0.5 * np.square(0.01-out_o1)
L_2 = 0.5 * np.square(0.99-out_o2)
L = L_1+L_2
print("Loss={}".format(L))
例えば、w5の勾配を計算する際には、
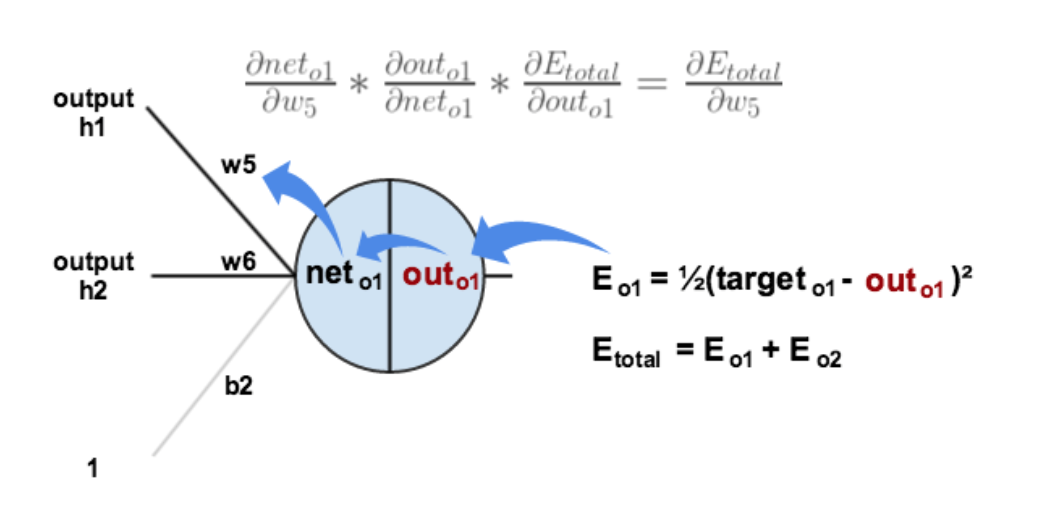
誤差逆伝播法でw5の勾配を求める
∂w5∂L=∂outo1∂L∂neto1∂outo1∂w5∂neto1 ∂outo1∂Lを計算する
L=21(targeto1−outo1)2+21(targeto2−outo2)2 合成関数の微分g(f(x))=g′(f(x))f′(x)によって
∂outo1∂L=2∗21(targeto1−outo1)∗−1+0 d_out_o1 = -(0.01-out_o1)
print("d_out_o1={}".format(d_out_o1))
d_out_o1=0.7065932011681534
∂neto1∂outo1を計算する
outo1=sigmod(neto1) Sigmoid関数の微分は f′(x)=f(x)(1−f(x)) なので
∂neto1∂outo1=outo1(1−outo1) d_net_o1 = out_o1*(1-out_o1)
print("d_net_o1={}".format(d_net_o1))
d_net_o1=0.20308738520773184
∂w5∂neto1を計算する
neto1=w5∗neth1+w6∗neth2+b2∗1 ∂w5∂neto1=neth1 d_w5= d_out_o1*d_net_o1*net_h1
print("d_w5={}".format(d_w5))
パラメータを更新する
w5+=w5−η∂w5∂L 以上の計算例には、2層ネットワークの場合の損失関数の勾配を誤差逆伝播法で計算できました。各層での勾配計算がチェーンルールに従っているため、層数が増えても理論的には同じ流れで処理できますため、任意の層数のネットワークに拡張することができます。
順伝播: 入力データが層を通過して出力に達するまで順番に計算が行われます。
損失の計算: ネットワークの最終出力(予測値)と実際のラベルとの誤差(損失)を損失関数で計算します (δjL=zj−dj)
逆伝播: 各隠れ層では、l(=L-1, L-2,...)でのδ(l)を、δ(l)=(∂z(l)∂z(l+1)⋅δ(l+1))⋅f′(zl)のように、次の層からの勾配を逆伝播させ、チェーンルールを使って計算します。
パラメータの更新:逆伝播によって計算された勾配δ(l)を用いて、各層の重みとバイアスを更新します。


