Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

機械学習の基本概念

1教師あり学習

機械学習は、コンピュータが大量のデータを学習することで、データの中に潜むパターンと規則性を抽出する技術です。ここで、「学習」は、観察されたデータをモデルに適合させるための調整可能な「パラメータ」を与えるために行われます。

機械学習は「教師あり学習」や「教師なし学習」、「強化学習」などの枠組が存在します。ここでは、教師あり学習に注目します。

教師あり学習（Supervised Learning）では、入力データ（特徴量）とそれに対応する正解ラベル（目標値）のペアを使用してモデルを訓練します。

モデルは、入力データと正解ラベルの間の関係やパターンを学習し、未知の入力データに対して正しい予測や分類を行うことが期待されます。テキスト分類、構文解析、機械通訳などの様々な自然言語処理タスクは、教師あり学習の問題として定式化できます。

教師データで学習した入出力の関係性がラベルを持たない未知の入力データにも使えるような関係性である必要があります。このように未知のデータにも対応できる性質を 汎用性 と言います。

高い推定精度を持ちかつ汎用性の高い関係性を見つけるのは教師あり学習の目的になります。

2機械学習のデータ構造

2.1学習データ、検証データとテストデータ

教師あり学習ではデータセットを「学習データ」、「検証データ」、「テストデータ」の3つに分けて使うのが一般的です。

  • 学習データ（Training Data）:モデルのパラメータを調整するために使用されます。学習データから、モデルがデータのパターンや関連性を「学び」ます。

  • 検証データ（Validation Data）: 検証データを使用してモデルの性能を評価し、その結果に基づいてハイパーパラメータを調整することができます。

  • テストデータ（Test Data）: このデータセットは、学習や検証のプロセスには一切使用されず、モデルの最終的な性能を評価するためだけに使用されます。テストデータを使用してモデルの性能を評価することで、実際の未知のデータに対するモデルの予測性能を推定することができます。

3機械学習モデルの評価指標

機械学習のモデルが良いか悪いかを評価するための評価基準は「評価指標」と言います。

4回帰タスク評価指標

yiy_iはii個目サンプルの真の値、pip_iはii個目サンプルの予測値とすると、

  • MAE（Mean Absolute Error）:平均絶対誤差

MAE=1N⋅∑i=1N∣yi−pi∣MAE = \frac{1}{N} \cdot \sum_{i=1}^{N} |y_i - p_i|
(1)

  • RMSE（Root Mean Squared Error）: 平均二乗誤差平方根

RMSE=1N⋅∑i=1N(yi−pi)2RMSE = \sqrt{\frac{1}{N} \cdot \sum_{i=1}^{N} (y_i - p_i)^2}
(2)

5分類タスク評価指標

分類タスクの評価指標は、よくある二分類タスクで説明します。分類の実際値と予測値は下記の４種類があります。

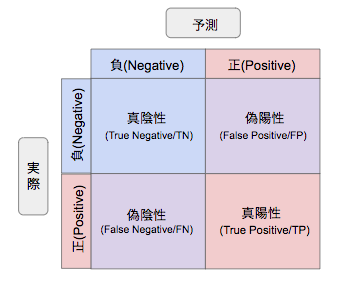
  • TP：True Positive 真陽性

  • FN：False Negative 偽陰性

  • FP：False Positive 偽陽性

  • TN：True Negative 真陰性

5.1正解率（Accuracy）

正解率は、正や負と予測したデータのうち、実際にそうであるものの割合です。

Accuracy=TP+TNTP+FP+TN+FN{Accuracy= \frac{TP+TN}{TP+FP+TN+FN} }
(3)

5.2適合率（Precision）

適合率は、正と予測したデータのうち，実際に正であるものの割合です。

Precision=TPTP+FP{Precision= \frac{TP}{TP+FP} }
(4)

5.3再現率（Recall）

再現率は、実際に正であるもののうち，正であると予測されたものの割合です。

Recall=TPTP+FN{Recall = \frac{TP}{TP+FN} }
(5)

5.4F-1値（F-1 score）

F値は、再現率と適合率の調和平均です。

F=2⋅Recall⋅PrecisionRecall+Precision{F = \frac{2\cdot Recall \cdot Precision}{Recall+Precision} }
(6)

6過学習

過学習(Overfitting)とは、データの傾向に沿うようにモデルを学習させた結果、学習時のデータに対してはよい精度を出すが、未知データに対しては同様の精度を出せないモデルが構築されてしまうことです。

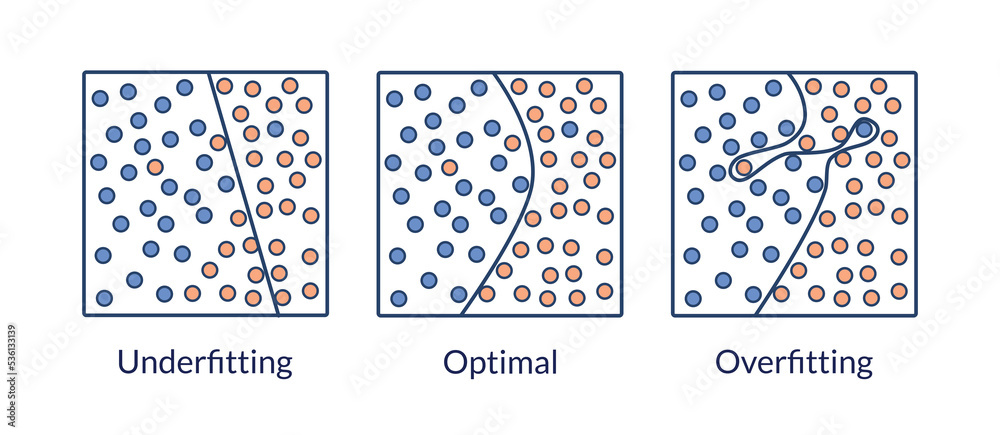
過学習を防ぐための一つの方法としては、交差検証法を使うことです。

交差検証とは、1つのデータを訓練データと検証データに分けるときに複数の分け方をして平均をとるという方法です。　データの分け方を複数作ることでリスクを分散し、訓練データと検証データの傾向の違いにより生じる過学習を最小化します。

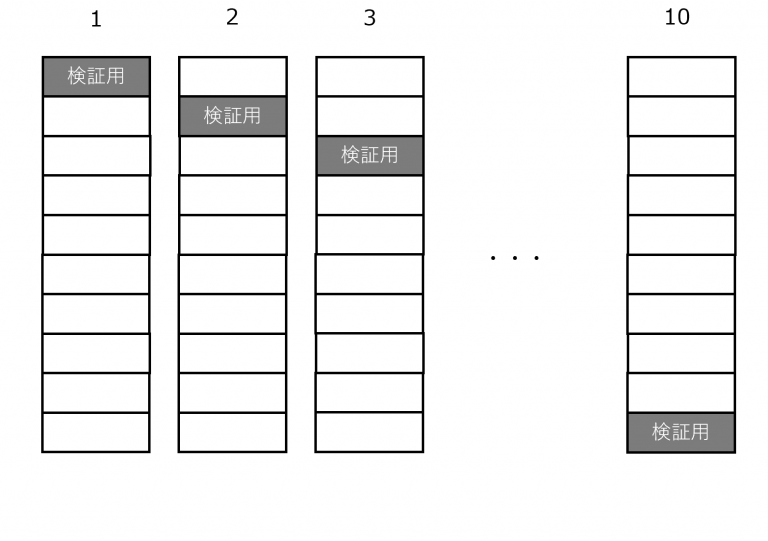
最もよく使われるK-交差検証では、

  • 全体データをK個にデータを分割します。

  • A～Kまであるうち、最初にAを検証データにしてB～Kのデータから予測モデルを作成。

  • Bを検証データにしてAとC～Kのデータから予測モデルを作成という流れで順番にK回検証していきます.

7機械学習のハイパーパラメータ

機械学習のハイパーパラメータは、学習アルゴリズムの動作を制御するためのパラメータです。

これらのハイパーパラメータは、モデルの学習プロセスの前に設定され、学習中には通常変わりません。ハイパーパラメータの設定に応じてモデルの精度やパフォーマンスが大きく変わることがあります。

ここでは、多くの機械学習・深層学習モデルに共通しているくつかのハイパーパラメータを紹介します。

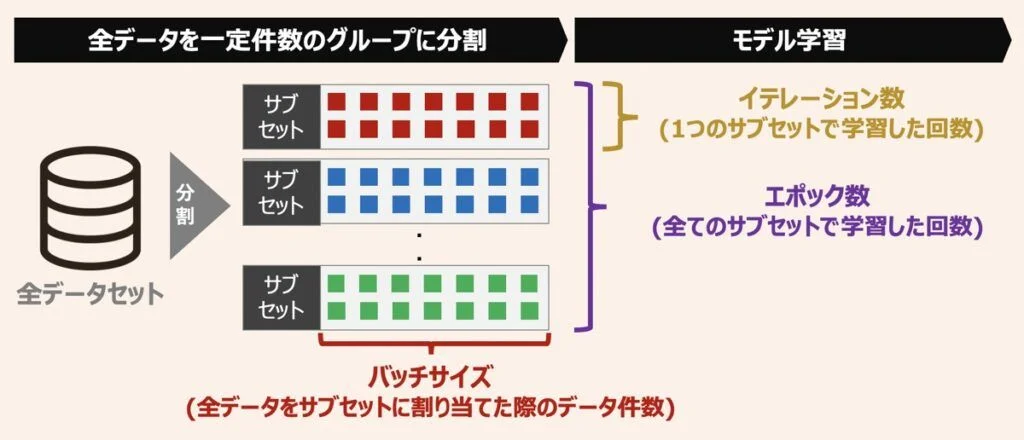
7.1バッチサイズ

機械学習のにおける「バッチ」は、学習アルゴリズムに一度に供給されるデータのサブセットを指します。「バッチサイズ」とは、学習プロセスにおいて、一度にモデルに供給されるサンプルの数を指します。

  • バッチ学習: 全ての学習データを利用して学習する手法です。つまり、バッチサイズはトレーニングデータの全サンプル数と等しくなります。この方法の利点は、計算が効率的であることですが、大量のメモリが必要になることや局所的な最適解にトラップされやすいという欠点もあります。

  • オンライン学習:ひとつひとつの学習データごとに学習処理を行います。具体的には、n個の学習データx1,x2,…,xnx_1, x_2, …, x_nからランダムに1つの学習データxix_iを抽出し、その1つのデータをモデルに投入します。オンライン学習は一件ずつの計算処理を採用しているため、常に更新される最新データ情報も柔軟に取り入れることができます。一方で、パラメータの更新をデータ一件ごとに行うので、学習を安定させることが難しいのもオンライン学習の懸念点です。

  • ミニバッチ学習: バッチ学習とオンライン学習の中間のような学習手法であり、データをミニバッチという小さなグループに分割してモデルを学習します。バッチ学習は、計算効率とメモリの使用のバランスが良いこと、および学習の収束速度が適切であるため、一般的に最も使用される方法です。

7.2エポック(epoch)数

機械学習・深層学習ようにパラメータの数が多いものになると、訓練データを何回も繰り返する必要があります。エポック数とは、学習において、データセットを何週繰り返してパラメータを調整するかを表す数を指します。1エポックは、トレーニングデータセット全体が一度、モデルを通過することを意味します。

例えば、データ件数が1000件で、バッチサイズが100なら、10回繰り返すと、1000件のデータに相当する件数分処理したことになります。この１単位のことを「エポック」と呼びます。

一般的には、エポック数が増えるほどモデルは訓練データに適応しやすくなります。しかし、エポック数が大きすぎると過学習のリスクが高まります。適切なエポック数を選ぶことで、モデルの性能を最大限引き出すことができます。

7.3イテレーション (Iteration)

イテレーション数はデータセットに含まれるデータが少なくとも1回は学習に用いられるのに必要な学習回数であり、バッチサイズが決まれば自動的に決まる数値です。先程の1000件のデータセットを100件ずつのサブセットに分ける場合では、イテレーション数は10となります。

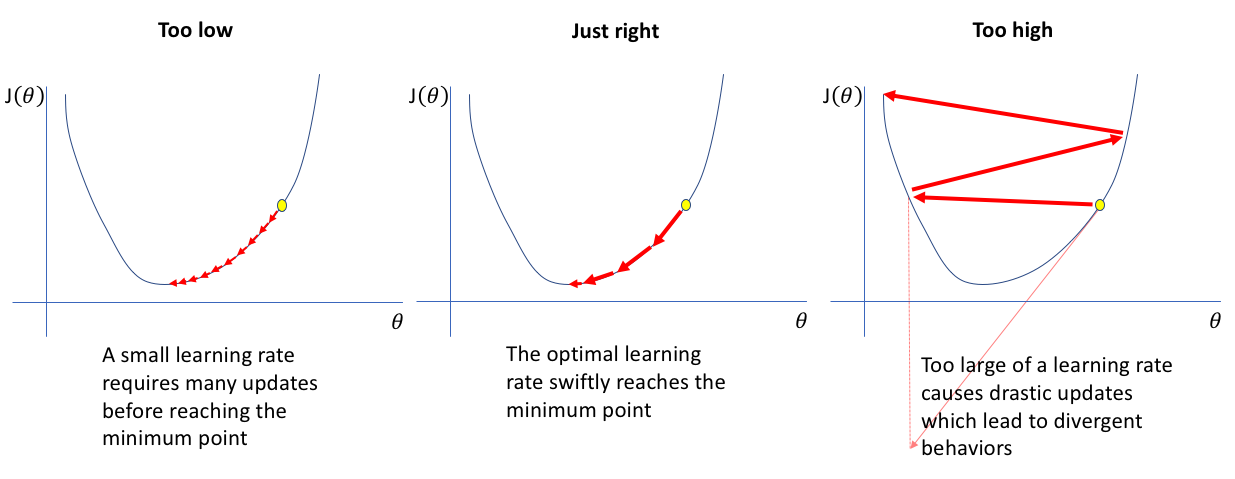
7.4学習率(Learning Rate)

学習率とは、機械学習の最適化において、重みパラメータを一度にどの程度変化させるかを表すハイパーパラメータのことです。

機械学習とは、反復的に重みパラメータを変更していきますが、学習率の値が高いほど一度に変更する重みパラメータの大きさが大きくなるので学習のスピードは上がり、反対に低ければ学習のスピードは下がります。

Source
import numpy as np
import math
import plotly.graph_objects as go
from plotly.subplots import make_subplots

# ===== ハイパーパラメータ（hyperparameter） =====
sample_size = 200     # トレーニングデータ数
batch_size = 20     # バッチサイズ
lr = 0.01            # 学習率
epochs = 1           # 1エポックのみ（全データを1回学習）

# ===== データ生成 =====
np.random.seed(42)
X = np.linspace(0, 10, sample_size)
y = 2 * X + 1 + np.random.randn(sample_size) * 1.0  # 真の関係: y = 2x + 1 + ノイズ

# ===== モデルのパラメータ（parameter） =====
w, b = 0.0, 0.0

# ===== 自動調整設定 =====
num_iters = len(X) // batch_size
cols = min(5, num_iters)
rows = math.ceil(num_iters / cols)

# ===== Plotly版 plt.subplots 相当 =====
fig = make_subplots(
    rows=rows, cols=cols,
    subplot_titles=[f"Iteration {i+1}" for i in range(num_iters)],
    horizontal_spacing=0.05, vertical_spacing=0.12
)

# ===== 学習ループ =====
for t in range(num_iters):
    # --- ランダムにbatchを選択 ---
    batch_idx = np.random.choice(len(X), batch_size, replace=False)
    X_batch, y_batch = X[batch_idx], y[batch_idx]

    # --- 学習前の予測線 ---
    y_pred_before = w * X + b

    # --- 勾配計算 ---
    y_pred_batch = w * X_batch + b
    dw = -2 * np.mean(X_batch * (y_batch - y_pred_batch))
    db = -2 * np.mean(y_batch - y_pred_batch)

    # --- パラメータ更新 ---
    w_new = w - lr * dw
    b_new = b - lr * db

    # --- 学習後の予測線 ---
    y_pred_after = w_new * X + b_new

    # --- subplotの位置 ---
    row = t // cols + 1
    col = t % cols + 1

    # ===== データ描画 =====
    # 全データ（灰色）
    fig.add_trace(
        go.Scatter(
            x=X, y=y, mode='markers',
            marker=dict(color='lightgray', size=5),
            name='全データ',
            showlegend=(t == 0)
        ),
        row=row, col=col
    )
    # 現在のバッチ（赤）
    fig.add_trace(
        go.Scatter(
            x=X_batch, y=y_batch, mode='markers',
            marker=dict(color='red', size=8),
            name='バッチデータ',
            showlegend=(t == 0)
        ),
        row=row, col=col
    )
    # 更新前（青）
    fig.add_trace(
        go.Scatter(
            x=X, y=y_pred_before,
            mode='lines',
            line=dict(color='blue', dash='dash'),
            name='更新前',
            showlegend=(t == 0)
        ),
        row=row, col=col
    )
    # 更新後（赤）
    fig.add_trace(
        go.Scatter(
            x=X, y=y_pred_after,
            mode='lines',
            line=dict(color='red'),
            name='更新後',
            showlegend=(t == 0)
        ),
        row=row, col=col
    )

    # 回帰式（テキスト表示）
    xref = "x" if t == 0 else f"x{t+1}"
    yref = "y" if t == 0 else f"y{t+1}"
    fig.add_annotation(
        x=0.05, y=0.95,
        xref=f"{xref} domain", yref=f"{yref} domain",
        text=f"y = {w_new:.2f}x + {b_new:.2f}",
        showarrow=False,
        font=dict(size=12, color="black")
    )

    # パラメータ更新
    w, b = w_new, b_new

# ===== レイアウト =====
fig.update_layout(
    title=f"線形回帰の学習過程（sample_size={sample_size}, batch_size={batch_size}）",
    height=400 * rows,
    width=1500,
    showlegend=True,
)

fig.show()
Loading...
基礎知識
自然言語処理の基礎
基礎知識
数学基礎